전자기학 및 광학 기초 이론(4) - 편광의 수학적 표현

• 편광의 발생

편광되어 있지 않은 빛이 다른 매질의 경계면에서 반사 또는 복굴절 매질을 투과하는 경우에 편광될 수 있다. 그밖에 편광판을 통과시키거나 대기 중의 분자에 의한 산란에 의해서도 편광이 발생한다.

 

1. 반사에 의한 편광

편광되어 있지 않은 빛이 굴절률 n1인 매질에서 굴절률 n2인 매질로 입사하는 경우에 입사각이 브루스터 각이 되면 반사된 빛은 편광된다. 

브루스터 각(또는 편광각)은 스코틀랜드의 물리학자 데이비드 브루스터(David Brewster, 1781년~1868년)에 의해 발견된 현상으로, 빛이 굴절률이 다른 두 매질 사이를 지날 때, 보통 그 경계면에서 반사가 일어난다. 하지만 어떤 편광 상태의 빛이 특정한 입사각으로 입사되면 경계면에서 반사되지 않는데, 이 특정한 입사각이 브루스터 각으로, 각도에서는 편광된 빛의 전기장이 입사되는 평면과 나란하여 반사되지 않는 것이다. 이 편광 상태의 빛은 p-편광(p-polarized) 상태라고 하는데, 입사되는 평면과 평행(parallel)하므로 붙여진 이름이다. 빛이 입사된 평면과 수직인 상태로 편광되어 있다면 s-편광(s-polarized) 상태라고 한다. 따라서 무편광 상태의 빛이 브루스터각으로 입사되면, 반사된 빛은 항상 s-편광 상태가 된다.

 

2. 복굴절을 이용한 편광

빛이 굴절률이 서로 다른 한 물질에서 다른 물질로 들어갈 때 그 경계면에서 진행 방향이 꺾이는 현상을 굴절이라고 한다. 복굴절은 굴절과 달리 두 개로 나누어져 꺾이는 현상이다. 방해석이나 몇몇 보석류와 같이 방향에 따라 굴절률이 다른 결정체에서는 입사한 빛의 파장이 같더라도 굴절률이 달라 빛이 갈라진다. 복굴절 된 두 개의 광파 중 하나는 굴절의 법칙을 만족시키나 다른 하나는 굴절의 법칙을 만족시키지 않는다. 한 방향으로 진행하는 빛에 대해서 두 가지 편광상태의 속도가 다른 현상을 복굴절이라고 하며 이런 특성이 있는 결정을 복굴절체라고 부른다.

 

편광되지 않은 빛이 복굴절성 매질을 통과할 때 수직편광 성분과 수평편광 성분의 진행속도가 다르다. 따라서 두 편광 성분의 빛은 위상차를 가지게 된다. 즉, 굴절된 빛은 위상차에 의해서 다른 두 개의 빛으로 나뉘어 진행하는데 이들은 서로 수직인 직선편광이다.

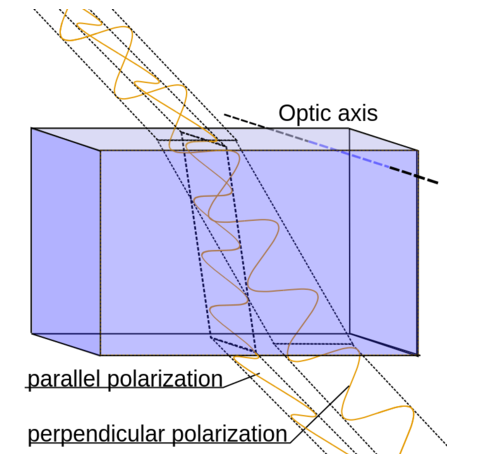
따라서 적당한 방법으로 한 방향 직선편광을 없애면 나머지 방향의 직선편광이 얻어진다. 한쪽 방향 편광을 없애지 않고 복굴절 매질의 두께(통과 거리)를 조절하면 투과한 후의 두 빛의 위상차를 조절하여 합성할 수 있다. 이로부터 원형편광이나 타원편광을 얻을 수 있다. 그러나 복굴절성 물질로 들어올 때와 나갈 때의 경계면에서 두 번의 굴절이 일어나서 통과 전과 통과 후의 빛의 진행 방향에는 변화가 없다.

 

대표적인 복굴절 물질인 방해석을 사용하여 편광프리즘을 만든다. 전기석을 이용한 전기석판 등의 편광자도 있다. 편광프리즘은 한쪽 굴절광을 반사시키며, 전기석판은 한쪽 굴절광을 많이 흡수하여서 투과광을 직선편광이 되게 한다. 전기석판은 특정한 편광면을 가지는 편광만을 통과시키는 검광자(Analyzer)로 사용할 수 있다.

 

• 편광의 표현

1. Jones vector와 Jones matrix

존스 행렬(Jones Matrix)은 빛의 편광을 기술해 주는 이차원 벡터 존스 벡터(Jones Vector)를 다루기 위한 행렬 표현식이다. 이 방법은 1941년 미국의 물리학자 존스(R. C. Jones)에 의해 고안되었다. 빛이 광학 소자를 투과할 때 그 광학소자의 광학적 특성을 2×2 존스 행렬로 표현할 수 있는데, 빛의 존스 벡터에 이 존스 행렬을 곱하면 투과한 빛의 편광상태를 계산할 수 있다.

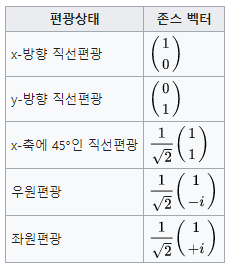
Jones Vector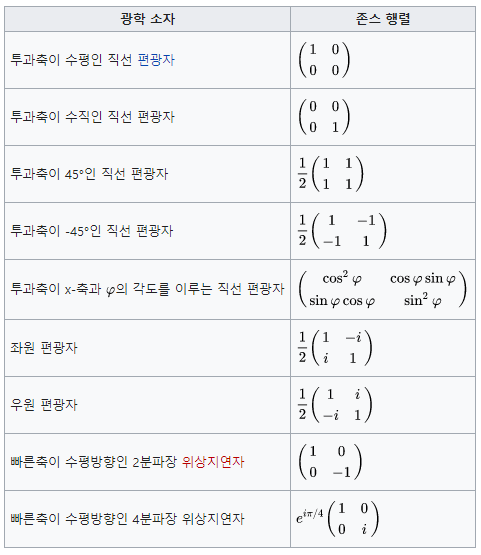

Jones Matrix

2. Stokes vector와 Mueller matrix

뮬러 행렬(Mueller matrix)은 완전 편광되지 않은 빛의 편광상태를 기술하는 스토크 벡터(Stokes vector)를 다루기 위한 행렬 표현식이다. 이 방법은 1943년 매사추세츠 대학교의 물리학 교수 한스 뮬러에 의해 고안되었다. 완전 편광된 빛은 뮬러 행렬이나 보다 단순한 존스 행렬로 계산할 수 있지만, 편광되지 않았거나 부분 편광된 빛은 뮬러 행렬로 풀어야만 한다. 완전편광의 경우엔 빛의 세기(intensity)보다는 진폭(amplitude)과 관계되기 때문에 일반적으로 존스 계산식을 이용하여 계산한다.

Mueller Matrix

3. 푸앵카레의 구(Poincare sphere)

타원편광이 편광의 일반적인 상태이므로 타원의 기하학적인 모양으로 편광상태를 나타낼 수 있다. 푸앵카레 구는 반경 1인 구에 편광상태를 대응시킨 것이다. 일반적인 타원편광은 장축이 x축 방향으로 놓인 타원을 α만큼 반시계방향으로 회전하여 만든 타원을 따라서 전기장이 진동한다. 장축에 대한 단축의 비율, 즉 타원율은 tan ε 이다. 그림처럼 전기장이 시계방향으로 회전하는 경우 타원율이 + 값을, 반시계방향으로 회전하는 경우 - 값을 갖도록 정한다.

타원편광

 

푸앙카레의 구(Poincare sphere)

이러한 구면의 한 점으로 편광상태를 나타내는 것이 특히 유용한 것은 임의의 편광이 이 표면 위에서 균등하게 존재할 수 있다는 것이다. 무수히 많은 편광상태가 혼재된 경우에는 복소수 표현이나 존스 벡터로 취급하기 곤란하다. 이 경우 구면으로 국한하지 않고 내부로 확장하면 혼재된 편광도 다룰 수 있게 된다. 특정한 한 편광은 반경이 1 인 구면 위에 표시되지만 이들을 벡터적으로 평균을 취한 것은 내부의 한 지점일 수 있으므로 혼재된 편광상태는 구 내부로 표시된다. 이것이 바로 푸앵카레 구(Poincare sphere)이다. 원점은 전혀 편광되지 않은 상태인 무편광이고 내부의 다른 점은 부분편광을 나타낸다. 바깥으로 오면 편광이 된 정도가 점진적으로 커져서 거리가 1 이 되면 완전하게 편광된 상태가 된다. 따라서 원점에서의 거리를 편광의 척도로 삼을 수 있다. 이를 편광도(degree of polarization)라 한다.