물질의 광학적 성질(1) - 물질의 유전율 및 분산모델

앞서 논의된 굴절률 등의 현상을 이해하기 위해서는 그 밑에 깔려 있는 빛과 물질과의 상호 작용을 이해하여야 한다.

우선 빛에 대한 물질의 반응은 사용하는 빛의 광양자 에너지(또는 파장)에 따라 다르게 나타난다. u-wave근처의 전자기파에 대해서는 물질을 구성하는 분자들의 영구 쌍극자가 반응을 하고, 적외선 영역에서는 이온들의 상대적 움직임에 의한 반응이 일어나고, 자외선이나 가시광선 영역에서는 원자를 구성하고 있는 전자나 유도 쌍극자들의 반응으로 나타난다. 

금속과 같은 도체 내부에는 외부 전기장에 따라 자유롭게 움직일 수 있는 자유전자(free electron)가 있는 반면, 절연체라고 부르는 물질 속에는 구속된 전자(Bound electron)들 뿐이다. 이 구속된 전자들 역시 외부 전기장에 의해 영향을 받는데 우리가 사용하고자 하는 가시광선(visible)과 그 주변의 광양자 에너지를 가진 빛(근적외선: near IR, 근자외선: near UV)이 물질에 입사하면 전자기파의 전기장과 물질 속의 전자들이 서로 상호작용을 하게 된다. 따라서 대부분의 Ellipsometry에서 측정하는 광현상들은 이들 전자들과의 상호작용의 결과이다. 

 

1. 물질의 유전율

유전체란 유리와 같이 구속된 전자만 있는 물질을 일컫는다. 물질에 전기장이 가해지면 내부의 핵과 전자가 서로 반대 방향으로 편향되거나, 물 분자와 같은 영구 쌍극자들은 전기장의 방향으로 정렬한다. 이로 인해 유전체 내부에 전기 쌍극자 모멘트(electric dipole moment)가 유도되는데, 이러한 현상을 편극(polarization)이라 한다. 편극의 세기는 단위 부피당 쌍극자 모멘트인 전기 편극 밀도(electric polarization density)은 다음과 같은 식으로 나타낸다.

편극이 일어나면 매질내의 전기장의 세기는 가해준 전기장에 비해 감소하는데, 이는 전기장은 가해준 전기장과 반대방향이기 때문이다. 이렇게 유도된 전기변위는 이러한 편극의 효과를 보정해주는 값이다.  

 

전기변위 D는 전기 편극 밀도 P와 외부에서 가한 전기장 E을 이용하여 다음과 같은 식으로 나타낸다.

여기서 ε0는 진공의 유전율이며 기본 물리상수로 8.854x10^-12F/m(단위 길이당 패럿)으로 패럿은 축전용량의 단위를 나타낸다. 유전율은 전기장에 따른 물질의 편극 크기에 따라 결정되며, 진공에서는 편극이 일어나지 않는다. 

유전율은 전기변위 D와 전기장 E의 비로 정의한다. 유전율은 매질에 따라서 달라지는데 유전율이 크다는 것은 매질 내에서 편극이 잘 일어난다는 의미이고, 유전율이 작다는 것은 편극이 잘 일어나지 않는다는 의미이다.

특별하게 즉각적으로 반응하는 선형의 균질한 등방의 매질의 경우에는 전기 편극 밀도는 다음 식과 같다. 

여기서 X(카이)는 전기 감수율(susceptibility)로 불리며 무차원의 매질의 고유 상수이다. 이러한 경우 전기 변위 D는 ε0(1+X)E가 되어 전기장 E와 비례하며, 그 비례상수가 ε=(1+X)ε0가 된다.

 

일반적인 경우에는 유전율은 상수가 아니다. 비선형 매질의 경우에는 전기장의 세기와 전기변위가 비례하지 않으며, 유전율은 전기장의 세기에 따라 변한다. 또 이방성(anisotropic, 비등방성)의 매질은 가해진 전기장의 방향에 따라서 편극의 크기가 달라진다. 이에 따라 유전율은 2차 공변텐서(second rank tenor)로서 나타난다. 대부분의 매질이 경우 전기장에 즉각 반응하지 않아 유전율을 시간의 함수 혹은, 진동수의 함수로 나타낸다. 이러한 경우 유전율을 복소수로 표현하기도 한다.

 

균질한 매질의 선형 유전율은 일반적으로 진공에서의 유전율과 비교하여 상대 유전율을 εr로 주어지며, 따라서 실제 유전율은 상대 유전율에 전기상수를 곱하여 구해진다.

이 유전율은 앞에서 언급한 복소굴절률과 연결시킬 수 있는데, 복소굴절률이 유전율의 제곱근과 비례한다는 식을 사용하면 다음과 같은 ε´=n2-k2, ε˝=2nk 관계식으로 나타낼 수 있다. 다시 한번 상기하면, n은 굴절률, k는 소광계수로 물질 속에서의 흡수정도를 나타낸다. 

 

2. 분산관계(dispersion relation)

매질 속에서 광학적 성질이나 유전적 성질이 빛의 광양자 에너지에 따라 달라지는 것을 분산(dispersion)이라고 한다. 백색광을 색깔별로 퍼지게 하여 무지개를 만드는데 사용하는 프리즘을 분산용 프리즘(dispersing prism)이라고 하는 것 역시 같은 의미이다. 

 

2-1. Lorenz harmonic oscillator 모델

어떤 유전체 물질에 전기장이 가해졌다고 가정했을 때, 물질 내부의 전자가 이에 영향을 받아 분극이 형성된다. 하지만 그렇다하여 이 전자들이 전기장에 의해 무작정 움직이는 것이 아니라, 핵과 연결되어 있고 전자들끼리 서로 충돌하기 때문에 움직임이 제한된다. 이러한 상황 속에서 핵과 전자의 상호작용을 용수철에 매달린 조그만 물체와 같이 Harmonic oscillator(Hooke's Law)로 보는 것이 Lorenz oscillator 모델이다. 

2-2. Drude 모델

앞서 설명했던 Lorenz 모델은 일반적으로 유전체의 전자에 대해 설명하는 모델이며, Drude 모델은 금속을 설명하는 모델이다.  금속의 전자는 유전체의 경우와는 다르게 핵에 속박되어 있지 않고 자유롭게 움직일 수 있다. 따라서 Lorenz 모델에서 용수철 상수만 0으로 두어 계산하면 된다.  

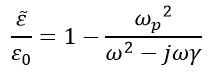
이러한 Drude모델은 실제 경우에 적용할 경우 한계점이 존재한다.

1. 낮은 주파수에서는 이론과 잘 맞지 않다. 금속 내에는 수많은 결합이 존재하는데, 에너지(빛)을 가하면 이 에너지를 흡수하게 된다. 그러나 Drude모델은 이러한 계산을 포함하고 있지 않다.

2. 높은 주파수에서는 자유전자 뿐만 아니라 핵에 속박되어 있는 전자도 영향을 끼친다. 주파수가 높은 때 속박된 전자도 자유전자와 마찬가지로 전기장에 반응을 하는데 그 때의 움직임도 전류에 포함된다. 즉 속박된 전자 및 자유전자 모두 전류를 흐르게 하며 Drude 모델에서는 자유전자들만 이 계산에 반영하였다.